JAKOŚĆ   

POJĘCIA OGÓLNE

Pojęcie JAKOŚĆ w odniesieniu do wyrobów i usług jest bardzo podobne do pojęcia POGODA. Występuje zawsze, potocznie domyślamy się skrótu myślowego z dodatkiem: korzystna, dobra. Rozu­mienie tego skrótu często nie jest dla ludzi takie samo. Dobra pogoda co innego znaczy dla żeglarza, co innego dla rolnika czy miłośnika wycieczek rowero­wych. Produkt wysokiej jakości może dla jednego klienta znaczyć bardzo trwały, dla drugiego wielo­funkcyjny, a dla innego największe znaczenie będą miały walory estetyczne. Definicja brzmi następują­co: Jakość jest to zespół cech i właściwości wyrobu lub usług, decydujących o zdolności wyrobu lub usługi do zaspokojenia stwierdzonych lub przewi­dywanych potrzeb. Poziom jakości to każda względ­na miara jakości, otrzymana w wyniku porównania wartości zaobserwowanych z odpowiednimi warto­ściami określonymi w wymaganiach. Wartość liczbowa poziomu jakości wskazuje zwykle stopień zgodności lub niezgodności, w szczególności z wymaganiami specyfikacji lub warunkami kontroli wyrywkowej.

Należy też wyjaśnić pojęcie SPECYFIKACJA. Jest to dokument, wyszczególniający wymagania, z którymi wyrób lub usługa powinny być zgodne. Jeśli to możliwe, wskazane jest, by wymagania były wyrażone liczbowo, w określonych jednostkach, łącznie z ich ograniczeniami. Dotyczy ona bezpo­średnio wskazanej właściwości jakościowej, a nie warunków, jakie kryteria przyjęcia ma spełnić.

Do określeń charakterystycznych dla oceny jakościowej używa się terminu: NIEZGODNOŚĆ, czyli niespełnienie ustalonych wymagań. Niezgod­ności powinny być w zasadzie klasyfikowane w myśl stopnia ważności. Natomiast WADA to niespełnienie wymagań związanych z zamierzonym użytkowa­niem. Jednostka wadliwa to jednostka, mająca jed­ną lub więcej wad, ale nie tylko. W pewnych przy­padkach szereg uchybień lub niezgodności może -kumulując się - uczynić jednostkę wadliwą. Trzeba teraz wyjaśnić termin: UCHYBIENIE jako odstęp­stwo właściwości od zaplanowanego poziomu lub stanu, niepowodujące niezgodności z wymagania­mi lub niemające wpływu na zgodne z przeznacze­niem użytkowanie wyrobu lub usługi. Poziom uzy­skanej cechy jakościowej okupiony jest zawsze ja­kimiś kosztami. Idealny stan nie jest możliwy ze wzglę­dów ekonomicznych i często także fizycznych. Uchy­bienia zwykle powinny być określane specjalną nazwą (np. ślad po wypychaczach, zapadnięcie, linie łączenia materiału itp.). Wskaźnikiem stopnia dotkliwości lub ważności uchybień może być opis identyfikacyjny, pomiar wielko­ści cechy lub jakakolwiek inna, od­powiednia skala oceny.

Należy rozróżnić dwie metody oceny cech jakościowych. METODA ALTERNATYWNA rejestruje wystę­powanie - lub nie - pewnej cechy albo właściwości w każdej jednostce należącej do zbioru i zliczanie liczby jednostek z tą cechą lub przypadków występowania w jednostce, grupie jednostek, na powierzchni itp. ME­TODA LICZBOWA mierzy i rejestruje wartości licz­bowe cechy jakościowej każdej jednostki, należącej do rozpatrywanego zbioru. Pociąga to za sobą przyporządkowanie pomiarom określonego rodzaju cią­głej skali.

TROCHĘ STATYSTYKI

W statystyce używa się pojęcia prawdopodo­bieństwa. Dla prawdopodobieństwa równego 0 wydarzenie nie może zaistnieć. Natomiast prawdo­podobieństwo wynoszące 1 znaczy, że wydarze­nie nastąpi na pewno. Łatwo się domyślić, że praw­dopodobieństwo wydarzenia p=0,25 oznacza, że w populacji równej 100 wystąpi ono w 25 przypad­kach. Możemy powiedzieć, że dla całej populacji reprezentacyjna jest próba utworzona z wybranych losowo przypadków. Na temat większej populacji możemy wyciągnąć wnioski na podstawie próby, która powinna być na tyle istotna, by była repre­zentatywna, ale nie tak duża, by narażała na nie­uzasadnione koszty. Stwierdzono, że dla wyciągnię­cia wiarygodnego wniosku zwykle wystarczy pró­ba o liczności co najmniej 50. Ale dla wyciągania wniosków w bardzo zróżnicowanej populacji, lub gdy są trudności w zachowaniu warunków losowe­go wyboru, stosuje się próbę o liczności nawet 1000.

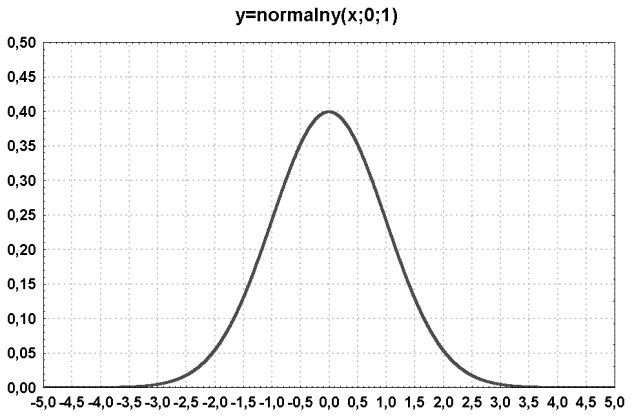
Różne cechy przedmiotów wykazują rozrzut swojej wartości. Jabłka wiszące na drzewie mają różne wymiary, różny jest bezawaryjny przebieg samochodu oraz różna grubość produkowanej folii. Rozrzut tych wielkości ma pewien charakter. Prze­biega on w sposób jak na rysunku 1:

                        RYS 1. Krzywa rozkładu normalnego Gaussa - gęstości prawdopodobieństwa

Dla jednoznacznego określenia każdego nor­malnego rozkładu wystarczają tylko dwa parametry: średnia arytmetyczna oraz odchylenie standardowe. Dla łatwiejszego przedstawienia zależności na wykresie przyjęto średnią wynoszącą 0 (zero), a odchylenie standardowe dla tego przypadku 1 (jeden). Średnią arytmetyczną każdy potrafi obli­czyć. Odchylenie standardowe można obliczyć kalkulatorem lub na komputerze za pomocą, np. programu EXCEL. Dla dociekliwych sposób obliczenia przedstawia się następująco:

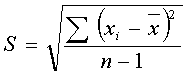
S - odchylenie standardowe

x_i  - wartość mierzonej właściwości dla po­miaru _" i" (i =1,2,3, ...n)

  - wartość średnia (w naszym przykładzie to 0)

n  - liczność zbioru

Można powiedzieć, że odchylenie standardowe określa przebieg krzywej i znajduje się ono w punkcie jej przegięcia. Ponieważ rozważamy wartości z próbki, to gdy będzie ona reprezentatywna, odchylenie standardowe z całej populacji będzie takie samo. Także inne reprezentatywne próbki z tej samej populacji będą miały to samo odchylenie standardowe oraz średnią. Dla ciekawości rozważmy przypadek: różne wielkości zebranych jabłek utworzyły wykres o krzywej podobnej do profilu wielbłąda dwugarbnego. Świadczyć to może o szczepie­niu drzewa dwoma gatunkami jabłek lub zbiorem z dwóch drzew.

Między 1s a -1s zawiera się 68,3% populacji, między 2s a -2s zawiera się 95,4% populacji, nato­miast poza 3s a -3s zostaje tylko 0,27% populacji. Ten ostatni zakres nazywa się granicami naturalnymi.

Przykładowe dane dla 50 pomiarów masy kształtek wtryskowych (w gramach) - tabela 1:

 Tabela 1. Masa kształtek wtryskowych

Jeżeli zakres tych danych podzielimy na kilka klas, z zależnością ilości w klasie na poszczególne zakresy, to możemy otrzymać wykres słupkowy zwany HISTOGRAMEM (rysunek 2):

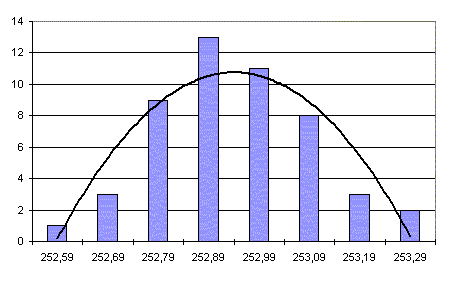
 Rys 2. Histogram danych z tabeli 1

Wykreślona linia trendu wyraźnie potwierdza, że zbiór danej próbki ma charakter rozkładu nor­malnego. Obliczona średnia to 252,89 gramów, odchylenie standardowe to 0,1568. Granice natu­ralne tego zbioru (-3s do 3s) to: 252,42g i 253,36g, czyli w tych granicach powinno znajdować się 99,73 % jednostek całej populacji.

Jeżeli te wyżej opisane kształtki zostały po­brane z procesu wzorcowego, to znaczy takiego, który gwarantuje wymaganą jakość, to dla innej próby, której średnia oraz odchylenie standardo­we będą takie same, możemy przypuszczać, że jakość też będzie też odpowiednia (jak w procesie wzorcowym).

Trzeba zdefiniować kilka innych wielkości, po­trzebnych do śledzenia populacji, w naszym przypad­ku wyrobów, za pomocą podzbiorów (prób).

MEDIANA to wartość środkowa. Jest to miara tendencji centralnej, dla której połowa obserwacji (50%) leży powyżej tej wartości, a druga połowa poniżej jej wartości. Jeśli liczba obserwacji w próbie jest parzysta, wówczas mediana jest obliczana jako średnia z dwóch wartości leżących pośrodku. Me­diana ma dużą zaletę, nie trzeba nic liczyć (jak dla średniej), wystarczy dla próby nieparzystej odrzucić zbędne dane. Inną wielkością opisującą próby, jest rozstęp. Rozstęp jest również jedną z miar zmienno­ści. Jest on wyliczany jako różnica pomiędzy największą i najmniejszą wartością zmiennej.

Istnieje zależność, że średni rozstęp obliczo­ny z wielu prób

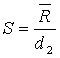
S- odchylenie standardowe próby

d₂ - współczynnik zależny od wielkości pró­by, można go znaleźć w normie

PN-ISO 8258 + AC: Karty kontrolne Shewarta

ZDOLNOŚĆ PROCESU

Podstawą systemów zapewnienia jakości zgod­nych z pakietem norm ISO 9000 jest samokontrola i stosowanie zapisów, potwierdzających wykonanie wszystkich czynności przy możliwej identyfikacji. By te zapisy miały rozsądną objętość, trzeba posługi­wać się metodami statystycznymi.

Dla uzyskania wyrobu o jakości na stałym, wysokim poziomie łatwiej i taniej nadzoro­wać proces, niż sprawdzać jego wynik koń­cowy. Nie znaczy to jednak, że rezultat każ­dej operacji nie jest najlepszym sprawdzia­nem poprawności procesu. Rachunek eko­nomiczny i wzajemne zależności parame­trów warunkują właściwy wybór diagnozo­wanej wielkości, mającej decydujący wpływ na spełnienie warunków specyfikacji .

SPC (ang. Statistical Process Control ) - statystyczne sterowanie procesem jest narzędziem do uzyskania pewności, że proces jest niezmienny. Statystycznie ure­gulowany proces (pod statystyczną kon­trolą) to stan, w którym zmienność między obserwowanymi wynikami badania próbki może być przypisana zespołowi przyczyn losowych i który nie ulega zmianom w cza­sie (przebiega tylko w granicach zależnych od stałych czynników przypadkowych).

Generalnie na pytanie, czy proces jest prawidłowy, tzn. wytwarzamy wyrób o po­trzebnej jakości, SPC jednak nie odpowia­da. Można nadzorować prawidłowy proces (spełniający całkowicie wymagania), jak i dający wyrób wadliwy. Miarą pewności, że proces spełnia wymagania, jest zdolność procesu: C_pk zdolność maszyno­wa: C_m. Wartości te można wyzna­czyć, jeśli znamy tolerancję tego parametru i będą one określały, ile razy w tolerancji mieści się 6 od­chyleń standardowych.

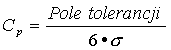
C_p dotyczy procesu w dłuższym przedziale czasowym. Dla krótkiego czasu, zwykle jednorazowej próby o liczności co najmniej 50, wyznacza się zdolność ma­szynową według tego samego wzoru. Nietrudno się domyślić, że łatwiej spełnić ten warunek. C_m po­winno być zwykle wyższe o wartość 0,33 niż C_p (po 1 odchyleniu standardowym więcej po każdej stro­nie).

Znaczy to, że jeśli C_p i C_m wynoszą 1, to 99,73% populacji mieści się w polu tolerancji, w tym przypadku jeszcze średnia populacji musi zgadzać się z wartością nominalną oczywiście, gdy zakres tolerancji od nominału w górę i w dół jest tej samej wielkości.

Dla C_p=1 proces jest zaledwie wydolny, jako minimum akceptuje się C_p=1,33. Aby wykazać, że proces ma odpowiednią wydolność, gdy średnia i nominał są przesunięte, określa się C_pk i C_mk (kry­tyczne) od strony mniejszej wartości (dla 3 s). C_pk i C_mk dopiero w pełni wskazują pewność produkcji, z parametrem w założonych, wymaganych grani­cach. Z praw statystyki wynika, że C_pk=2 to pew­ność, że nie wystąpi więcej niż 4 ppm (części na milion, czyli 0,0001%) braków i to przy założe­niu, że średnia próbki i całej populacji mogą być przesunięte o 1. Stosunek C_mk do C_pk określa wpływ czynników zakłócających w zależności od czasu. Często w specyfikacji podana jest wartość C_pk i C_mk, której utrzymanie w procesie produkcyjnym należy wykazać zlecającemu za pomocą odpowiednich do­kumentów. Przykład - tabela 2:

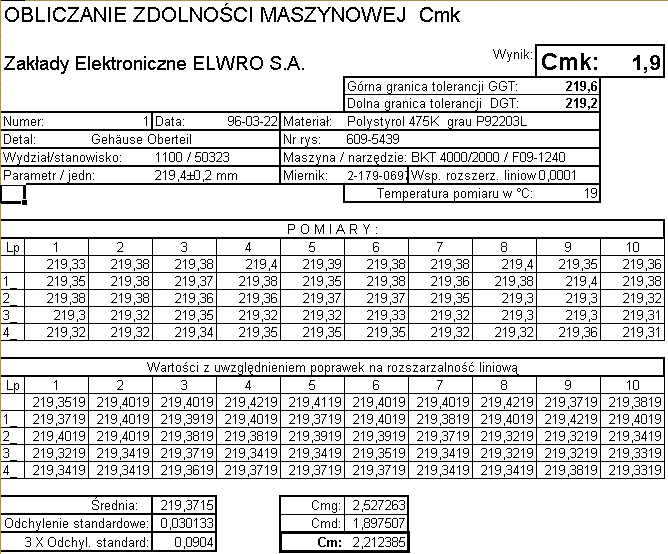
Tabela 2.Przykład wymiarów z próby kształtek wtryskowych [mm] oraz określania C_mk

Przedstawiona tabela to fragment prostego arkusza kalkulacyjnego Excel. Obliczenia takie moż­na zrobić za pomocą kalkulatora z funkcjami staty­stycznymi lub na piechotę zwykłym kalkulatorem. Tabela pokazuje zadawalającą zdolność maszyno­wą C_mk=1,9, która została wybrana jako mniejsza ze zdolności procesu górnej C_mg i dolnej C_md. Zdolność C_m jest bardzo dobra i w przypadku, gdy trzeba zapewnić właśnie taką wystarczy poprawić wymiar w formie, bo sam proces jest do tego odpowiedni. Gdy nawet samo C_m jest za małe na nasze oczeki­wania, trzeba poprawić proces.

Do badań końcowych wyrobów lub badań jakościowych dostarczonych surowców stosuje się powszechnie metody statystyczne, używając metod alternatywnych lub tańszych na podstawie liczbowej oceny właściwości. Te ostatnie metody potrafią odpowiedzieć na to samo pytanie, co metody alter­natywne, ale przy zmniejszonej liczności prób.

Przedstawiona wyżej ocena zdolności procesu jest oceną potencjału procesu produkcyjnego w zakresie możliwości utrzymania jakości na wyznaczonym poziomie. Najkorzystniejsze jest jednak sterowanie lub, jak kto woli, nadzorowanie procesu. W następnym numerze zostanie przedstawiona kolejna część artykułu. Zajmiemy się w niej właści­wym problemem: SPC, czyli statystycznym stero­waniem procesami.

 Literatura

1. A. Iwasiewicz, Statystyczna kontrola jakości w toku produkcji. Systemy i procedury, PWN, Warszawa 1985.

2. PN-ISO 3534-2, Statystyka. Statystyczne ste­rowanie jakością. Terminologia i symbole

3. PN-ISO 8258 + AC1, Karty kontrolne Shewharta.

4. H. Helmers, SPC- Statystyczne sterowanie pro­cesem. Praktyczne Sterowanie Jakością. Alfa Weka 1997

5. W. Linkę, Statystyczne prowadzenie procesu (SPC) w przetwórstwie tworzyw sztucznych, Mat. Sym­pozjum: Plastech'94, s.123-146.

6. Z. Filipowski, SPC - Statystyczne sterowanie procesem wtryskiwania tworzyw sztucznych, Postęp w przetwórstwie tworzyw sztucznych, Politechnika Czę­stochowska 1997, s.237-243

Zdzisław Filipowski

 Wróć na górę